Musical Interval Qualities

This article may contain compensated links. Please read the disclosure for more info.

Become a musical interval expert!

In this music theory lesson, you will learn about the qualities of intervals in music. You'll understand the difference between a major and minor interval and how to tell the difference between a perfect, augmented, and diminished interval.

How to Measure a Musical Interval

Musical intervals are measured in two steps:

First, by counting the distance from one note to the next (the first interval note being 1). This is the "numerical" name of the interval.
The second step is to determine how large or small an interval is. An interval of a third, for example, can be either major or minor. This is the "quality" of the interval.

With a little help from our friends, the accidentals (sharps & flats), our interval can become even bigger, called augmented, or smaller, called diminished.

Whoa! Wait, don't freak out! There are tricks that you will learn here. But first things first:

If you don't already know how to quickly identify the interval with its numerical value (Unison, 2nd, 3rd, 4th, etc.) I recommend you go to this lesson first, where you'll learn to identify basic intervals with numbers. I'll be waiting for you here when you're done!😉

Musical Scale Intervals

The easiest way to learn about the different sizes, called quality, of musical intervals, is to use the major scale as a template.

In a C major scale, if you start from C and measure it against one note at a time, from the scale, the intervals will all be either Major or Perfect.

From C-D is the interval of a Major 2nd,
C-E is a Major 3rd,
C-F is a Perfect 4th,
C-G is a Perfect 5th,
C-A is a Major 6th,
C-B is a Major 7th,
and C-C is a Perfect Octave.

Using the major scale (any major scale will do) is a great tool. You can use it to remember exactly how large a Major or a Perfect interval is. In this way, you don't have to memorize exactly how many semitones and tones apart each interval quality is!

Simply use the C major scale as your "ruler" and compare.

For example, C-D is an example of a Major Second. But how large exactly? A whole step (or two half-steps/semitones). So all major seconds are a whole step (whole tone) apart.

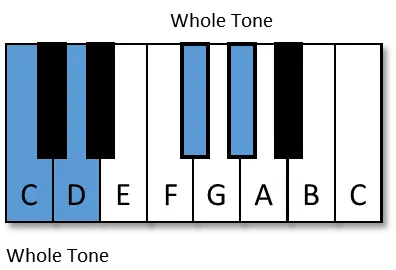
Let's Take a Closer Look

From C to itself (!) the interval is called a Prime or Unison. It's a Perfect Unison.

From C to D is the interval of a 2nd. Since this 2nd is a whole tone apart; it is called a Major 2nd.

From C to E is a Major 3rd. Two whole tones apart.

C to F is a Perfect 4th. 2 1/2 tones apart.

C to G is a Perfect 5th. 3 1/2 tones apart.

C to A is a Major 6th. 4 1/2 tones apart.

C to B is a Major 7th. 5 1/2 tones apart.

C to C is a Perfect Octave. 6 tones apart.

So this was the "base-line". Now we have something to compare with!

Major Intervals

As we saw, 2nds, 3rds, 6ths, and 7ths are called Major intervals when you use the exact distance of whole and halftones from the major scale as we did above.

So, you can just refer to the major scale when you want to know how many tones and semitones apart each Major interval is.

Perfect Intervals

We also learned that the 4th, 5th, and Octave are called Perfect when using the "major scale method". A Unison (from one note to the same note) is also a Perfect interval.

Music Intervals on the Staff

The following method to learn the different intervals and their qualities is to look at the notes on a musical staff. But, before we do, let's check out this piano keyboard:

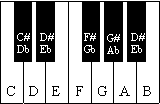
On a piano keyboard, we see the pattern of all the 12 pitches in Western musical notation. All the keys are a semitone (half step) apart.

If we look at only the white keys, we have the note names of the 7 basic notes: A B C D E F G. You'll notice that between these basic or "white" notes, not all intervals are the same (not all have a black key between them).

All are a whole tone apart except between E-F and B-C where there is only a semitone or a half step. (There is no black key between!) This is important to remember! All the basic notes are a whole tone apart except between E-F and B-C!!!

Memorized that? OK. Let's look at the musical staff and the notes on it.

All notes are a whole tone apart...except between E-F and B-C here as well, of course!

On a music staff, all notes may look as they are the same distance apart....but now you know they aren't!

So, quickly learn to find those semitones and remember where they hide: between E-F and B-C.

Minor Intervals

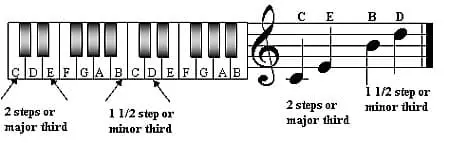
On a musical staff (please observe that we're not using any sharps or flats yet!), you'll find Minor, Diminished, and Augmented intervals. At least a few.

For example, from B-D, there is a 3rd, but it is only 1 and 1/2 semitone apart. This is called a Minor 3rd.

How would you know this? By comparing with the size of a Major 3rd in the major scale method above, which is 2 whole tones/steps apart. And from E-F there is a 2nd, but it's tiny, only a semitone, so it's called a Minor 2nd.

Major and minor thirds on a piano keyboard and staff.

Augmented and Diminished Intervals

There is also a weird musical interval of a 4th, between F and B. It is called a Augmented 4th because it's a semitone bigger than a Perfect 4th.

Augmented and perfect fourths on a piano keyboard and staff.

And check out the 5th between B and F. It is a semitone smaller than a Perfect 5th, so it is called a Diminished 5th.

Diminished and perfect fifths on a piano keyboard and staff.

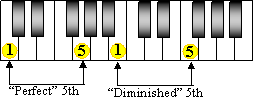
Both these intervals are exactly 3 whole tones apart. They are also called "tritone" intervals.

Summary

OK. So let's summarize what we've seen so far. The basic intervals (using no black keys or accidentals) can be divided into two main groups:

2nds, 3rds, 6ths and 7ths. These can be either Major (big) or Minor (small).
Unison, 4ths, 5ths, and Octaves. They are called Perfect. The only exception is the two intervals between F-B, and B-F, where there is a "bigger" 4th, called Augmented, and a "smaller" 5th, called Diminished.

Send in the Accidentals!

Now the fun bit! Each musical interval can, of course, be altered using sharps and flats, also called accidentals!

So, what happens then?

When adding accidentals, a musical interval can become even larger/smaller.

Major and Minor Intervals:

In order of size from smallest to largest:

Diminished->Minor->Major->Augmented

Perfect Intervals:

As we saw above, when using notes without sharps or flats, the Perfect Intervals (Unison,4ths, 5ths, and Octaves) are all Perfect...

Except for the intervals between F-B and B-F! These two intervals are called "tritones" since they are 3 tones apart! They are also "enharmonic" (sounding the same) even though one is a 4th (Augmented) and the other a 5th (Diminished).

By adding accidentals, we can make these intervals larger or smaller!

The sizes for Perfect intervals from smallest to largest:

Diminished->Perfect->Augmented