Music Interval Inversions

This article may contain compensated links. Please read the disclosure for more info.

Interval Inversions are a useful way to analyze musical intervals. By learning how to "turn intervals over" or invert them, you can quickly see what size and quality they have. In this basic music theory lesson, you'll learn how to do this.

What are Interval Inversions?

Inversions in music theory are when we flip things over! : )

You can invert chords and intervals, for example. When inverting intervals, you simply move one of the notes an octave higher or lower.

• If you move the lowest note, you move it an octave higher.
• If you move the highest note, you move it an octave lower.

Like this:

• Move the lowest note in the 3rd (F) an octave higher. Now the interval is inverted to a 6th.
• Or move the highest note in the 3rd (A) an octave lower. The interval is still inverted to a 6th.
• Likewise with a 2nd. Inverted it becomes a 7th, up or down it doesn't matter.

Using Interval Inversions to Analyze Intervals

We use interval inversions to analyze intervals. It is a "shortcut" if you like, to find the right number and quality of the interval much faster.

Look at these intervals:

• By inverting a unison, you get an octave.
• Inverting a 2nd turns it into a 7th.
• A 3rd turns into a 6th.
• And a 4th becomes a 5th.

So how is this useful?

It becomes extra useful when looking at interval qualities (major, minor, perfect, etc.) When the intervals are inverted, the quality becomes the opposite!

• For example, a Major 3rd inverted becomes a Minor 6th.
• A Major 7th becomes a Minor 2nd, and so on.
• The Perfect Intervals (Unison-Octave, 4th-5th) always stay perfect, though.

This means that you only have to memorize two intervals' sizes:

• the 2nd and 
• the 3rd!

From the Major Scale Intervals method, you learned that:

• A Major 2nd is a whole step/tone apart.
• A Major 3rd is two whole steps/tones apart.

Then, you automatically know that a Minor 2nd is a half step smaller, only a semitone. And a Minor 3rd is 1 1/2 steps apart.

So...

Let's say you quickly need to analyze this interval (the first one):

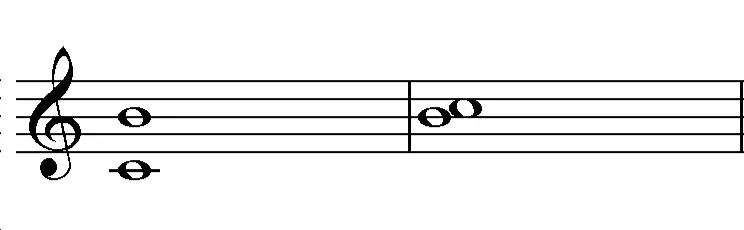
• Aha. It's a 7th. But how big exactly (also called "quality")?
• Invert it by moving C up an Octave. Now you have a minor 2nd (since there is only a semitone between B-C).
• So, the 7th is the opposite: a Major 7th!

You don't even need to count to know if it's a 7th, just invert it, and since it's a 2nd- you know that the original was a 7th. How quick is that!

Let's practice!

Here is a 6th (the first interval). How big exactly?

• Invert it (move E up an Octave) and we have a Major 3rd, since it's 2 whole steps between C and E.
• So the original interval is the opposite; a Minor 6th!

Now you can quickly analyze all 2nds, 3rds, 6ths and 7ths!

What About Perfect Interval Inversions?

Well, the Perfect intervals we don't really have to practice so much since they are all perfect...

A Perfect 5th becomes a Perfect 4th and vice versa. The same with Octaves and Unisons (which you wouldn't need to invert anyway- would you?)

The only exception of the 4ths and 5ths is between F-B and B-F where our in-famous tritone intervals are lurking.

The 4th between F and B is Augmented (large) and the 5th between B and F is Diminished (small).

Invert a Diminished 5th and you get an Augmented 4th and vice versa.

Using Accidentals

This lesson is about interval inversions with "white" notes or notes without accidentals (sharps and flats).

But it's good to know that all intervals could also become Augmented, or Diminished by using accidentals.. :)

Back to the Major and Minor Intervals

The best part is, that even the diminished intervals become augmented and vice versa when inverted. And you still only need to memorize how many tones (or semitones) a 2nd and a 3rd are, to compare with.

Example:

Analyze this interval:

That's an...aherrm...big interval...?

No... Invert it! And what do you get?

A # and C... A weird third.

But you know that a Major 3rd is two whole steps. This third is two semitones smaller. Still a 3rd, but a Diminished 3rd. Which makes the original interval an Augmented 6th!

That's it! No weird Intervals anymore!

ShareFacebookTwitterPinterestReddit

FacebookTwitterPinterestReddit